Sistemi a due corpi
In un primo approccio con le leggi del moto, si considera solitamente la dinamica di una sola particella soggetta a forze assegnate. Le leggi di Newton ci dicono come possiamo risolvere il problema del moto.
Tuttavia le situazioni reali in cui si può studiare il moto di una particella totalmente isolata dall'ambiente circostante sono rare. In generale occorre tener conto che essa interagisce con altre particelle presenti tramite forze di vario tipo: gravitazionali, elettriche, magnetiche...
Nel caso gravitazionale, assumere che il Sole sia fermo e ciascun pianeta si muova attorno ad esso indipendentemente dagli altri è solo una prima approssimazione della situazione, dove il Sole in realtà si muove per effetto della sua interazione con i pianeti e, inoltre, i pianeti interagiscono tra loro.

Nel caso della Luna e della Terra l’effetto è più evidente. Entrambi i corpi sono accelerati dalla reciproca interazione e il moto della Terra non è trascurabile. È un tipico problema a due corpi.

Essendo i sistemi composti da più particelle piuttosto difficili da studiare, si comincia con l'analizzare il moto di un particolare punto del sistema, detto centro di massa.
E' quello che si fa usualmente quando si applica a un corpo esteso la legge del moto F=ma, valida per un punto materiale. In questo caso si identifica il sistema con un suo punto, che è appunto il centro di massa.

Osservando questo tuffo in acqua, possiamo notare che il moto di un punto qualunque del corpo del nuotatore è, in generale, piuttosto complicato. C'è però un punto particolare (il centro di massa) il cui moto è molto più semplice e può essere studiato applicando la seconda legge di Newton. Le forze che si considerano agenti sul centro di massa sono quelle esterne applicate all'intero sistema, nel caso della tuffatrice sarà quindi la sua forza peso.
Centro di massa
La determinazione della posizione del centro di massa di un corpo di forma qualunque, magari non omogeneo (cioè che presenta parti di densità diverse), è tutt'altro che semplice. Tuttavia in alcuni casi particolari è facilmente individuabile.
Iniziamo con il definire il centro di massa per due punti materiali P1 e P2 di massa m1 e m2.

Fissiamo un sistema di coordinate e siano x1 e x2 le ascisse dei due punti materiali. Si definisce centro di massa del sistema il punto CM, situato sulla retta individuata da P1 e P2, la cui ascissa è tale che:

Nel caso particolare in cui le due masse siano uguali, il centro di massa si trova nel punto medio del segmento di estremi P1 e P2 o più in generale con il baricentro del sistema. Un corpo esteso omogeneo (di densità costante) può essere visto come sistema di moltissime particelle tutte di ugual massa; per esso quindi il centro di massa coincide con il baricentro matematico della figura. Ad esempio, il centro di massa di una sfera omogenea è il centro stesso della sfera.
Con i dati che abbiamo, possiamo dimostrare che il centro di massa del sistema Terra-Sole è interno al Sole, mentre quello del sistema Terra-Luna è interno alla Terra.


Per calcolare il centro di massa del sistema Terra-Sole, applichiamo la definizione fissando il sistema di ascisse ponendo lo 0 nel centro del Sole:

Il centro di massa è quindi interno al Sole, essendo la sua posizione minore del raggio solare. Possiamo ripetere il calcolo nel caso del sistema Terra-Luna, fissando lo 0 delle ascisse nel centro della Terra:

Anche in questo caso il centro di massa è interno alla Terra, essendo la sua posizione minore del raggio terrestre.
Proprietà del centro di massa
Vogliamo ora studiare il moto del centro di massa quando al sistema sono applicate delle forze esterne.
Come fatto in precendena, fissiamo un sistema di ascisse e prendiamo in considerazione due masse m1 e m2, rispettivamente nelle posizioni x1 e x2.

Supponiamo inoltre per comodità che le due particelle si muovano in una stessa direzione, quella dell'asse x.
Si può dimostrare che vale la seguente (vedi approfondimento):
Per il principio di azione e reazione, le forze interne si annullano. Nel membro di destra dell'equazione precedente rimarranno quindi solo le forze esterne al sistema.
Seconda legge di Newton per un sistema di particelle
Il centro di massa del sistema si muove come un punto materiale di massa uguale alla massa totale del sistema sul quale agisce la risultante delle forze esterne.
Segue che se il sistema è isolato, ovvero le particelle interagiscono solo tra di loro, allora il centro di massa si comporta come una particella libera e si muoverà di moto rettilineo uniforme oppure rimane in quiete.
Nel caso di un sistema formato da più di due particelle, si possono riproporre gli stessi concetti e quindi definire analogamente il centro di massa del sistema e la seconda legge di Newton.
Esempio
Un proiettile viene sparato da terra e ad un certo istante esplode in volo dividendosi in diversi frammenti. Com'è il moto del centro di massa del sistema formato dai frammenti dopo l'esplosione?
Risoluzione:
si trascuri l'attrito con l'aria. Le forze che agiscono sono la forza di gravità, le forze interne causate dall'esplosione del proiettile. Essendo forze interne, per il principio di azione e reazione annullano il loro contributo sul moto del centro di massa.
Quindi dopo l'esplosione, il centro di massa dei frammenti continua a muoversi lungo la stessa traiettoria parabolica che avrebbe seguito il proiettile se non fosse esploso.

Moto relativo dei due corpi
Finora non abbiamo ancora considerato il modo in cui le forze interne influiscono sul moto del sistema. Esse infatti, sebbene non contribuiscano al moto del centro di massa del sistema, determinano il moto relativo delle due particelle. Manteniamoci nella situazione del sistema Terra-Luna.

Per moto relativo si intende che, invece di studiare contemporaneamente il moto dei due corpi e quindi le due posizioni x1 e x2, ci si limita ad analizzare come varia la distanza tra i due corpi, che chiameremo x.
Si può dimostrare (vedi Approfondimento) che il moto relativo delle due particelle è governato dall'equazione del moto equivalente all'equazione del moto di una sola particella di massa ridotta μ soggetta ad una forza F.
La massa ridotta del sistema Terra-Luna è definita come:

L'equazione del moto relativo Terra-Luna diventa:

E' il solito problema di Keplero. La posizione relativa descrive un'orbita ellittica, quella che compete ad una particella di massa ridotta μ, soggetta alla forza di gravitazione. Una volta che si conosce il moto relativo di Terra e Luna e la posizione del centro di massa, si possono ricavare le posizioni di Terra e Luna nel tempo.

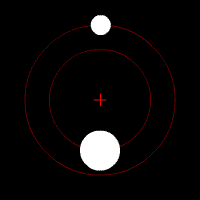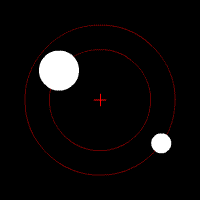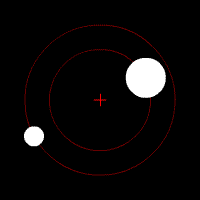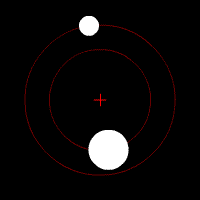
Terra e Luna descrivono delle ellissi intorno al centro di massa comune, di uguale eccentricità e di semiassi proporzionali al rapporto mL/mT.

Curiosità
Ecco come variano le orbite di due corpi celesti in reciproca attrazione al variare del rapporto delle loro masse: